Пружинный маятник в среде с сопротивлением

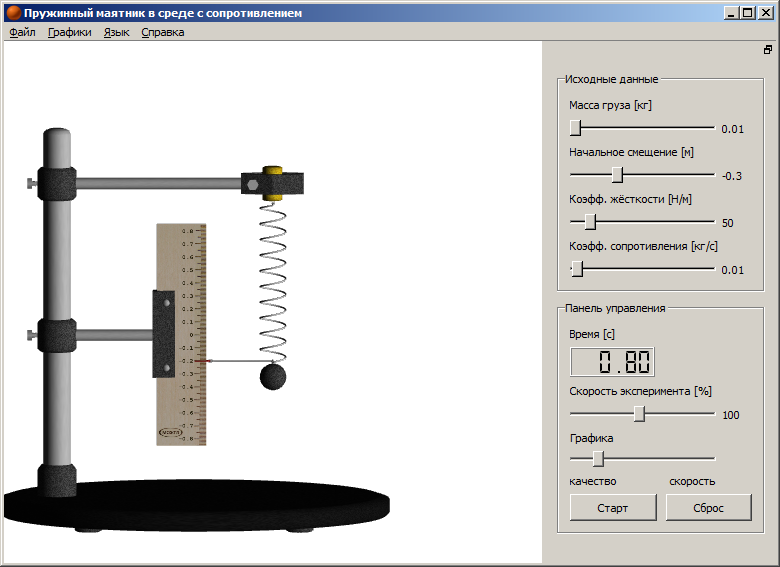
В программе моделируются свободные затухающие колебания пружинного маятника.

Существует возможность изменять следующие параметры модели:

Для удобства проведения эксперимента добавлены секундомер и возможность изменения скорости опыта, а так же линейка для измерения смещения груза от положения равновесия.

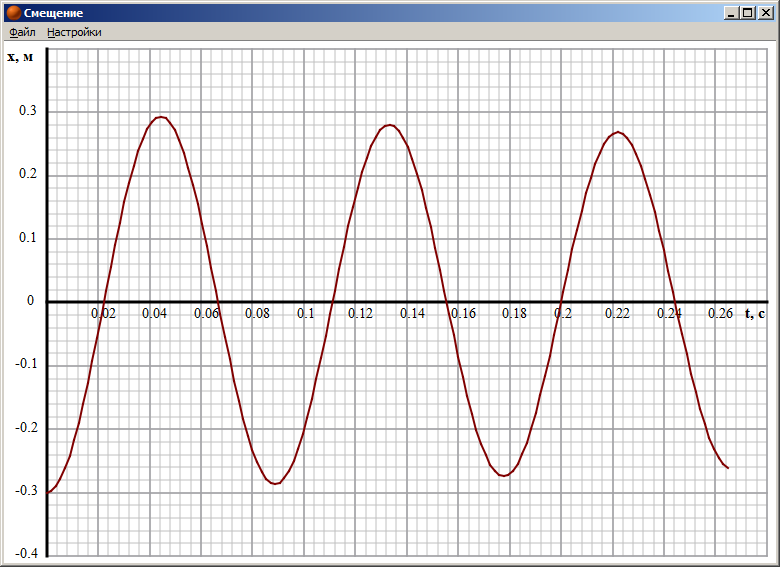
В программе могут быть выведены графики следующих зависимостей:

Скриншоты

Загрузка

Список изменений

Компилятор / Qt	ОС	Ссылка
MinGW 3.4.2, Qt 4.4.3	Windows 98 SE и выше	pendulum_qt4.4_mingw32.zip
MSVC 2017 x86, Qt 5.6.3	Windows XP SP3 и выше	pendulum_qt5.6_msvc2017_x86.zip
MSVC 2017 x64, Qt 5.6.3	Windows XP x64 SP2 и выше	pendulum_qt5.6_msvc2017_x64.zip
MSVC 2022 x86, Qt 5.15.5	Windows 7 x86 и выше	pendulum_qt5.15_msvc2022_x86.zip
MSVC 2022 x64, Qt 5.15.5	Windows 7 x64 и выше	pendulum_qt5.15_msvc2022_x64.zip
GCC 4.8.5 i486, Qt 5.6.3	GNU/Linux i486	pendulum_qt5.6_i486-linux-gnu.elf.gz
GCC 4.8.5 x86_64, Qt 5.6.3	GNU/Linux x86_64	pendulum_qt5.6_x86_64-linux-gnu.elf.gz
Clang 9.0.0 x86_64, Qt 5.15.5	GNU/Linux x86_64 (AppImage)	pendulum_qt5.15_x86_64-linux-gnu.AppImage
Clang 9.0.0 x86_64, Qt 5.15.5	GNU/Linux x86_64 (deb)	pendulum_1.2.0-1_amd64.deb
Apple Clang 13.1.6, Qt 5.6.3	Mac OS X 10.6 и выше (x86_64)	pendulum_qt5.6_clang64_libstdcxx.dmg
Apple Clang 13.1.6, Qt 5.15.5	Mac OS X 10.10 и выше (x86_64/AArch64)	pendulum_qt5.15_universal_target10.10.dmg

[v1.1] - 05 Dec 2021

Изменен идентификатор организации и домашняя страница, т.к. старый домен более не доступен
Обновлен модуль с общим кодом
Исправлена собираемость с Qt 5.10+
Добавлена базовая поддержка Qt 6.x (пока без аппаратного OpenGL)
Обновлены сборочные скрипты
Подготовлены сборки с Qt 5.15.2 для Windows, GNU/Linux и macOS

[v1.0] - 31 Dec 2016

Глобальный рефакторинг, в ходе которого исправлено множество мелких багов
Общий код вынесен в отдельный модуль, который теперь используется и в других проектах
Добавлена английская локализация
Подготовлены официальные сборки для GNU/Linux и macOS
Исправлены проблемы с текстурами для устаревших видеокарт
Доработан дизайн приложения
Добавлена кастомизация внешнего вида графиков
Изображения графиков и текущего состояния сцены теперь можно сохранять
Реализована базовая поддержка дисплеев с высоким разрешением
Реализована базовая поддержка управления сценой жестами типа Pinch и Pan

[v0.40] - 25 Aug 2015

Добавлен альтернативный софтверный рендер для систем, плохо поддерживающих OpenGL
Увеличена частота обновления изображения
Исправлено восстановление исходного состояния сцены
Обновлены ссылки на проект
Обновлены сборочные скрипты под Windows

[v0.39] - 05 Jan 2015

Построитель графиков перенесен с OpenGL на QPainter, исправлены найденные ошибки
Исправлены ошибки линковки при использовании Qt 5.4 в конфигурации -opengl dynamic
В сборочных скриптах под Linux добавлено экранирование переменных
Поправлены опции компиляции

[v0.38] - 24 Aug 2014

Добавлен антиалиасинг
Исправлены баги с освещением
Исправлены баги с непрорисовкой моделек из некоторых положений
Переписан построитель графиков

[v0.37] - 20 Aug 2014

Исправлен глюк с отображением шрифтов в Windows 98 (сломано в v0.36)
Улучшена поддержка системных шрифтов

[v0.36] - 07 Aug 2014

Добавлена совместимость с Qt5
Форма основного окна теперь одна для всех платформ
В основном окне теперь используются системные шрифты, если они поддерживают кириллицу
Добавлено управление с клавиатуры графическим виджетом, если он в фокусе
Начальное смещение можно регулировать точнее
Изменена стартовая позиция камеры на более удобную
В окне лицензии исправлены адреса ссылок, сами ссылки теперь кликабельны
Исправлены недоработки в меню "О программе"
Скриншоты в руководстве пользователя теперь лучшего качества и разные для разных платформ
Убрано все ненужное из файла проекта
Исправлены и доработаны сборочные скрипты
MinGW 4.8.x некорректно работал с __attribute__((packed)), заменено на #pragma pack
Убраны ненужные подключения <GL/glext.h>
Вместо <GL/glu.h> используется платформонезависимый <QtOpenGL>
Проект портирован под MSVC (протестировано на MSVC 2005 и MSVC 2013)
Исправлены все предупреждения компилятора
Исправлены найденные утечки памяти и переполнения
Бинарные билды теперь собираются в MSVC 2013 (кроме legacy), появиласть сборка для x64

[v0.35] - 09 Jan 2014

Исправлены и оптимизированы сборочные скрипты для Win32
В заголовок главного окна добавлена версия программы

[v0.34] - 01 Dec 2013

Убран скроллбар в окне с лицензией в Win32 версии
Добавлен пункт меню "О Qt"

[v0.33] - 11 Nov 2013

Улучшены низкополигональные модели
Изменен алгоритм вычисления значения коэффициента сопротивления от положения ползунка
Улучшено позиционирование в ползунках регулировки массы и смещения
Убрана автоматическая подстройка качества графики, ибо все равно работала не так, как задумывалось
Исправлены e-mail адреса на актуальные
Модели перенесены из каталога src/resources/data в src/resources/models

[v0.32] - 29 Oct 2013

Улучшены низкополигональные модели

[v0.31] - 27 Oct 2013

Добавлены текстуры уменьшенного разрешения
Улучшены низкополигональные модели

[v0.30] - 27 Oct 2013

Добавлены низкополигональные модели
Исправлен баг с неверным пропуском кадров при скорости эксперимента меньше 100%
Исправлено неверное изменение размеров графиков при геометрии окна, близкой к квадратной

Список предыдущих изменений, увы, не сохранился.

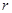	— коэффициент сопротивления среды,
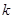	— коэффициент жёсткости пружины,
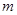	— масса груза,
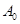	— начальная амплитуда,
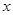	— смещение груза,
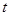	— время,
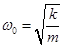	— циклическая частота свободных незатухающих колебаний,
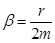	— коэффициент затухания,
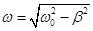	— циклическая частота свободных затухающих колебаний,
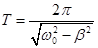	— период колебаний,
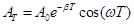	— амплитуда колебаний в момент времени, равный периоду,
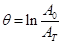	— логарифмический декремент,
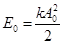	— энергия в начале эксперимента,
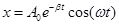	— смещение в текущий момент времени,
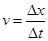	— скорость в текущий момент времени,
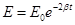	— энергия в текущий момент времени.

Пружинный маятник в среде с сопротивлением

Описание

Описание установки

Скриншоты

Загрузка

Список изменений

Модель